Real-Time Rendering
第五章 着色基础
渲染三维对象的图像时,模型不仅应具有适当的几何形状,还应具有所需的视觉外观。根据不同的需求,模型的视觉外观可以是真实感外观(外观接近真实物体)或是各种风格化外观。如下图所示,上面的图片是一种真实感外观渲染,下面的图片是一种风格化外观渲染。

本章将讨论照片级真实感渲染和风格化渲染的着色基础。
着色模型(Shading Models)
确认渲染对象外观的第一步是选额着色模型。着色模型用于描述对象应该如何根据对象表面法线、视角方向(view direction)和光照方向等因素来计算其外观(颜色)。
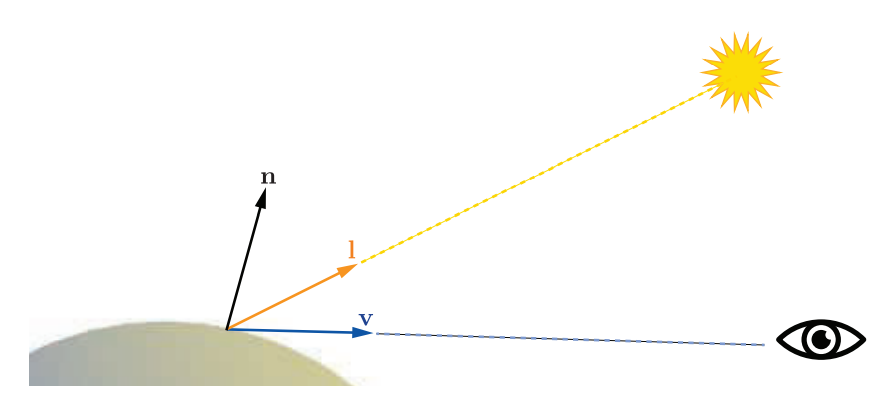
举个例子,我们将使用Gooch着色模型的变体。这是非真实感渲染的一种形式。
Gooch着色基本思想是将表面法线与光源的位置进行比较。如果法线指向灯光,则使用较暖的色调为表面着色,否则使用较冷的色调。介于两者之间的角度在这些色调之间进行插值,这取决于用户提供的表面颜色。如下图所示:

着色模型通常具有用于控制外观变化的属性(properties)。设置这些属性的值是确定对象外观的下一步。我们的示例模型只有一种属性,即表面颜色。
我们可以看一下模型本身的数学定义:
\[\mathbf{c}_{shaded}=s\mathbf{c}_{highlight}+(1-s)(t\mathbf{c}_{warm}+(1-t)\mathbf{c}_{cool})\]其中:
\(\mathbf{c}_{cool}=(0,0,0.55)+0.25\mathbf{c}_{surface}\),
\(\mathbf{c}_{warm}=(0.3,0.3,0)+0.25\mathbf{c}_{surface}\),
\(\mathbf{c}_{highlight}=(1,1,1)\),
\(t=\frac{(n\cdot l)+1}{2}\),
\(\mathbf{r}=2(\mathbf{n}\cdot\mathbf{l})\mathbf{n}-\mathbf{l}\),
\(s=(100(\mathbf{r}\cdot\mathbf{v})-97)^{\mp}\)。
该定义中的几个数学表达式也经常可以在其他着色模型中找到。着色操作中通常会进行Clamping操作,通常Clamping到0或Clamping在0到1之间。这里的标记是将高光混合因子\(s\)Clamping在0到1之间。点积运算符出现3次,每次出现在两个单位长度的向量之间,这是一个非常常见的模式。两个向量的点积是它们的长度与它们之间夹角的余弦的乘积。因此,两个单位长度向量的点积就是余弦,它是两个向量彼此对齐程度的度量。由余弦组成的简单函数通常是最令人愉悦和最准确的数学表达式,用于说明着色模型中两个方向(例如,光照方向和表面法线)之间的关系。
另一种常见的着色操作是基于0到1之间的标量值在两种颜色之间线性插值。该操作采用\(t\mathbf{c}_a+(1-t)\mathbf{c}_b\)的形式,随着\(t\)的值在1和0之间移动,它会在\(\mathbf{c}_a\)和\(\mathbf{c}_b\)之间进行插值。此形式在上面的模型中出现了两次,一次是在\(\mathbf{c}_{warm}\)和\(\mathbf{c}_{cool}\)之间插值,第二次在前面的插值结果与\(\mathbf{c}_{highlight}\)之间进行插值。线性插值在着色器中出现的频率很高,以至于在大多数着色语言中,它都是一个内置函数,称为lerp或mix。
向量\(\mathbf{r}=2(\mathbf{n}\cdot\mathbf{l})\mathbf{n}-\mathbf{l}\)是反射光向量,是光线\(\mathbf{l}\)关于法线\(\mathbf{n}\)的反射光线。尽管不像前两个操作那样常见,但是大多数着色语言也都具有内置的反射(reflect)功能。
通过将这些操作以不同的方式与各种数学表达式和着色参数组合在一起,可以为多种风格化和写实的外观定义着色模型。
光源(Light Sources)
光照对我们上面的示例着色模型的影响非常简单。但是现实世界中的光照可能非常复杂。可以有多个光源,每个光源都有自己的大小、形状、颜色和强度。间接光照会带来更多的变化。
相反,根据应用程序和视觉样式的需要,风格化的着色模型可以以多种不同方式使用光照。一些高度风格化的模型可能根本没有光照的概念,或者(例如我们的Gooch着色示例)可能仅使用它来提供一些简单的方向性。
其次,着色模型可以以二元方式对光的存在或不存在做出反应。即使用这种着色模型的表面在有光照时具有一种外观,在没有光照时具有另一种外观。区分这两种情况的标准有距光源的距离,阴影,表面是否背对光源(即法线与光线之间的角度大于90度)等因素。
进一步,从二元方式到能随光照逐渐变化的着色,可以用简单的插值来实现。例如:
\[\mathbf{c}_{shaded}=f_{unlit(\mathbf{n},\mathbf{v})}+k_{light}f_{lit}(\mathbf{l},\mathbf{n},\mathbf{v})\]上式可以简单的扩展为RGB光照颜色\(\mathbf{c}_{light}\):
\[\mathbf{c}_{shaded}=f_{unlit(\mathbf{n},\mathbf{v})}+\mathbf{c}_{light}f_{lit}(\mathbf{l},\mathbf{n},\mathbf{v})\]以及多个光源:
\[\mathbf{c}_{shaded}=f_{unlit(\mathbf{n},\mathbf{v})}+\sum_{i=1}^{n}\mathbf{c}_{light}f_{lit}(\mathbf{l_i},\mathbf{n},\mathbf{v})\]我们还可以将光在表面上的效果可视化为一组射线,其中射线击中表面的密度对应用于表面着色的光照强度。如下图所示,该图为光照表面的横截面。沿该截面入射到表面的光线之间的间距与\(\mathbf{l}\)和\(\mathbf{n}\)的夹角的余弦成反比。因此,入射到表面的光线的总密度与\(\mathbf{l}\)和\(\mathbf{n}\)的夹角的余弦成正比,正如我们前面所看到的,它等于这两个单位长度向量之间的点积。在这里,我们看到了为什么光照向量\(l\)与光的传播方向相反会很方便,否则我们将在执行点积运算之前将其取反。
当光线密度为正时,光线密度与点积成正比。负值对应于从表面后面发出的光线,是无效的。因此,我们需要先 将其Clamp点积为0。使用\(x^{+}\)表示,即将负值Clamp为0,我们会得到:
\[\mathbf{c}_{shaded}=f_{unlit}(\mathbf{n},\mathbf{v})+\sum_{i=1}^{n}(\mathbf{l}_i\cdot n)^{+}\mathbf{c}_{light_i}f_{lit}(\mathbf{l}_i,\mathbf{n},\mathbf{v})\]对于函数\(f_{lit}()\),最简单的选择是使其为常函数:
\[f_{lit}()=\mathbf{c}_{surface}\]代入后即得:
\[\mathbf{c}_{shaded}=f_{unlit}(\mathbf{n},\mathbf{v})+\sum_{i=1}^{n}(\mathbf{l}_i\cdot n)^{+}\mathbf{c}_{light_i}\mathbf{c}_{surface}\]该模型的lit part(即后半部分)对应于兰伯特着色模型(Lambertian shading model),该模型在理想的漫反射表面(即完全无光泽的表面)下运行。
接下来,我们将讨论几种流行类型的光源,它们有一个共同点:在给定的表面位置,每个光源仅从一个方向\(\mathbf{l}\)照射表面。即从着色表面的一个点来看,光源是一个无限小的点。但现实世界中的光源并非严格如此,但是大多数光源与被照明表面的距离较小,因此这是一个合理的近似值。
- 方向光(Directional Lights)
方向光(Directional Lights)是光源最简单的一种模型:\(\mathbf{l}\)和\(\mathbf{c}_{light}\)都是恒定的,除了\(\mathbf{c}_{light}\)可能会因阴影而衰减。方向光无位置。当到光源的距离相对于场景大小较大时,方向光具有不错的效果,例如被太阳照亮的场景基本上都可以用方向光。